题目大意
给定一棵以$1$号点为根、大小为$n$的有根树($n \le 10^5$),每一条边上有一个小写英文字母
给定$m$个询问,第$i$个询问包含一个长度为$t_i$的点集(元素可重,$\sum{t_i} \le 2 \cdot 10^5$),询问$\sum\limits_{a=1}^{t_i}{\sum\limits_{b=a+1}^{t_i}{lcp(a,b)}}$
定义$s_a$为从a出发走向根,将边上的字符按顺序写下来构成的字符串
定义$lcp(a,b)$为$s_a$与$s_b$的最长公共前缀
下面举一个栗子
若树长成这样:
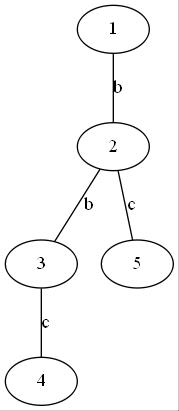
那么$s_5=cb,s_4=cbb$
更进一步,若某次询问的点集为$\{4,5\}$那么答案为$2$
解题报告
看到这种树上的字符串,我能想到AC自动机,或者广义后缀自动机
想了想AC自动机做不了,那就广义后缀自动机来做咯!
考虑后缀自动机上的Fail树
一个点的祖先实际上是这个点代表的字符串的后缀
那么题目中的$lcp(a,b)$就变成了$lca(a,b)$
于是对于每一次询问,我们建一个虚树出来
然后在虚树上DFS一次,统计一下答案就好啦!
另外,这题用后缀数组也可以做!
听武爷讲一讲,大概就是先把Trie树建出来
同时记录下每一次倍增的$Rank$数组(波兰表……)
然后就正常倍增,写法已经和罗穗骞的后缀数组的实现很不同了
Code
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 200009;
const int M = N << 1;
int n,m,E,head[N],nxt[M],to[M],col[M],pos[N],id[N];
inline int read() {
char c=getchar(); int ret=0,f=1;
while (c<'0'||c>'9') {if(c=='-')f=-1;c=getchar();}
while (c<='9'&&c>='0') {ret=ret*10+c-'0';c=getchar();}
return ret * f;
}
inline void Add_Edge(int u, int v, int c = 0) {
to[++E] = v; nxt[E] = head[u]; head[u] = E; col[E] = c;
to[++E] = u; nxt[E] = head[v]; head[v] = E; col[E] = c;
}
class Suffix_Automaton{
int cnt=1,ch[N][26],fail[N],vis[N],dep[N],sum[N];
int tot,arr[N],que[N],len[N],fa[N][20],_hash[N];
vector<int> G[N]; LL ans_tmp;
public:
inline int insert(int t, int cc) {
if (ch[t][cc] && len[ch[t][cc]] == len[t] + 1) return ch[t][cc];
int tail = ++cnt; len[tail] = len[t] + 1;
while (!ch[t][cc] && t) ch[t][cc] = tail, t=fail[t];
if (!t) fail[tail] = 1;
else {
if (len[ch[t][cc]] == len[t] + 1) fail[tail] = ch[t][cc];
else {
int nw = ++cnt, w = ch[t][cc]; len[nw] = len[t]+1;
memcpy(ch[nw], ch[w], sizeof(ch[nw]));
fail[nw] = fail[w]; fail[w] = fail[tail] = nw;
for (;ch[t][cc]==w;t=fail[t]) ch[t][cc] = nw;
}
} return tail;
}
inline void Build_Fail_Tree() {
memset(head,0,sizeof(head)); E = 0;
for (int i=2;i<=cnt;i++) Add_Edge(fail[i], i);
dfs(1, 1);
for (int j=1;j<20;j++) {
for (int i=1;i<=cnt;i++) {
fa[i][j] = fa[fa[i][j-1]][j-1];
}
}
}
inline LL solve(int nn) {
for (int i=1;i<=nn;i++) arr[i] = pos[read()];
sort(arr+1, arr+1+nn, [](const int &a, const int &b) {return id[a] < id[b];});
for (int i=1;i<=nn;i++) _hash[i] = arr[i];
int mm = nn; nn = unique(arr+1, arr+1+nn) - arr - 1;
for (int i=1;i<=nn;i++) sum[i] = 0;
for (int i=1,j=1;i<=mm;i++) {
while (arr[j] != _hash[i]) j++;
sum[j]++;
}
que[tot=1] = 1; int MX = 1;
for (int i=1,lca;i<=nn;i++) {
vis[arr[i]] = sum[i];
lca = LCA(que[tot], arr[i]);
while (dep[que[tot]] > dep[lca]) {
if (dep[que[tot-1]] >= dep[lca]) G[que[tot-1]].push_back(que[tot]);
else G[lca].push_back(que[tot]);
--tot;
}
if (que[tot] != lca) que[++tot] = lca;
if (arr[i] != que[tot]) que[++tot] = arr[i];
MX = max(MX, tot);
}
while (tot > 1) G[que[tot-1]].push_back(que[tot]), --tot;
ans_tmp = 0;
Get_Ans(1);
return ans_tmp;
}
private:
void dfs(int w, int f) {
static int id_count = 0;
id[w] = ++id_count;
fa[w][0] = f; dep[w] = dep[f] + 1;
for (int i=head[w];i;i=nxt[i]) {
if (to[i] != f) {
dfs(to[i], w);
}
}
}
int Get_Ans(int w) {
int ret = vis[w];
if (w > 1) ans_tmp += vis[w] * (vis[w] - 1ll) / 2 * len[w];
for (int i=G[w].size()-1,tmp;~i;i--) {
tmp = Get_Ans(G[w][i]);
ans_tmp += (LL)tmp * ret * len[w];
ret += tmp;
}
vis[w] = 0;
G[w].clear();
return ret;
}
inline int LCA(int a, int b) {
if (dep[a] < dep[b]) swap(a, b);
for (int i=19;~i;i--) if (dep[fa[a][i]] >= dep[b]) a = fa[a][i];
if (a == b) return a;
for (int i=19;~i;i--) if (fa[a][i] != fa[b][i]) a = fa[a][i], b = fa[b][i];
return fa[a][0];
}
}SAM;
void DFS(int w, int f, int t) {
pos[w] = t;
for (int i=head[w];i;i=nxt[i]) {
if (to[i] != f) {
int nt = SAM.insert(t, col[i]);
DFS(to[i], w, nt);
}
}
}
int main() {
n = read(); char pat[10];
for (int i=1,u,v;i<n;i++) {
u = read(); v = read();
scanf("%s",pat+1);
Add_Edge(u, v, pat[1] - 'a');
}
DFS(1, 1, 1);
SAM.Build_Fail_Tree();
for (int i=read();i;i--)
printf("%lld\n",SAM.solve(read()));
return 0;
}
Everyone loves what you guys are up too. Such clever work
and reporting! Keep up the excellent works guys I’ve incorporated you guys to my own blogroll.
I’m not sure where you’re getting your info, but great topic.
I needs to spend some time learning more or understanding
more. Thanks for magnificent information I was looking for this info for my mission.
I like the helpful information you provide in your articles.
I’ll bookmark your blog and check again here
regularly. I am quite sure I will learn many new stuff right here!
Good luck for the next!
I was pretty pleased to uncover this site.
I wanted to thank you for your time for this particularly wonderful read!!
I definitely loved every bit of it and I have
you saved as a favorite to see new things on your site.
of course like your web site but you need to test the spelling on several of your posts.
A number of them are rife with spelling issues and I in finding
it very bothersome to inform the truth then again I will definitely come
back again.
I’ve read a few just right stuff here. Definitely
price bookmarking for revisiting. I wonder how much attempt you place to
create such a great informative site.
Thanks for sharing such a nice thinking, paragraph is nice, thats why
i have read it fully
Hi! Do you know if they make any plugins to protect against hackers?
I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?
It’s awesome in favor of me to have a web site, which is
useful in favor of my experience. thanks admin
This is a topic which is near to my heart… Cheers! Exactly where
are your contact details though?
Good post. I’m dealing with a few of these issues as well..
I am really loving the theme/design of your site. Do you ever run into any web browser compatibility issues?
A number of my blog visitors have complained about my website not
working correctly in Explorer but looks great in Firefox.
Do you have any solutions to help fix this issue?
The following time I read a weblog, I hope that it doesnt disappoint me as much as this one. I mean, I know it was my option to learn, but I actually thought youd have one thing attention-grabbing to say. All I hear is a bunch of whining about one thing that you would fix when you werent too busy on the lookout for attention.
An interesting discussion is definitely worth comment. There’s no doubt that that you ought to write more on this issue, it might not be a taboo
subject but generally folks don’t speak about these issues.
To the next! Many thanks!!
You really make it appear so easy along with your presentation however I in finding this topic
to be really one thing that I feel I might by no means understand.
It kind of feels too complex and very extensive for me.
I’m looking forward on your subsequent submit, I’ll try to
get the dangle of it!
Today, while I was at work, my cousin stole my iPad and tested to see if it can survive
a thirty foot drop, just so she can be a youtube sensation. My iPad is now broken and she has 83 views.
I know this is totally off topic but I had to share it with someone!
Its like you read my thoughts! You seem to know a lot about this,
like you wrote the e book in it or something.
I think that you could do with some percent
to drive the message home a bit, but instead of that, this is fantastic blog.
A fantastic read. I’ll certainly be back.
Hello, i think that i saw you visited my site thus i came to “return the favor”.I’m attempting to find things to enhance
my website!I suppose its ok to use some of your ideas!!
Thank you for any other magnificent post. Where else may anyone get that type of
info in such an ideal means of writing? I have a presentation subsequent week, and I am at the
search for such info.
I am actually happy to read this webpage posts which contains plenty of
useful facts, thanks for providing these data.
Peculiar article, totally what I wanted to find.
Stunning quest there. What occurred after? Good luck!
Thanks in favor of sharing such a fastidious idea, post is pleasant,
thats why i have read it entirely
I’d like to find out more? I’d love to find out more details.
Way cool! Some very valid points! I appreciate you writing this write-up plus the rest of the site is extremely good.
bookmarked!!, I love your web site!
I was suggested this blog via my cousin. I’m now not positive
whether or not this submit is written by way
of him as nobody else recognize such specific about
my trouble. You are amazing! Thanks!
I like the valuable information you provide in your articles. I’ll bookmark your weblog and check again here frequently. I am quite certain I will learn many new stuff right here! Best of luck for the next!
I think this is a real great post.Really thank you! Want more.
Awesome blog article.Thanks Again. Want more.