退役前一直想把莫比乌斯反演与容斥原理统一在一起,奈何自己水平不足,只能作罢。
这次把《组合数学》、《具体数学》、《初等数论》的相关内容读了一遍,总算是完成了这个遗愿:
mobius_and_inclusion_exclusion_principle
Download:http://oi.cyo.ng/wp-content/uploads/2018/03/mobius_and_inclusion_exclusion_principle.pdf
拓展阅读1:http://blog.miskcoo.com/2015/12/inversion-magic-binomial-inversion
拓展阅读2:http://vfleaking.blog.uoj.ac/blog/87
Category: 算法笔记
Latex入门文档
很久没用latex写过东西了,再加上编辑器从Emacs换成了VScode,于是为了写下面↓那个slide就找了点资料熟悉一下。
找到了这一份:https://liam0205.me/2014/09/08/latex-introduction/
感觉写得很好,而且作者似乎是CTeX的主要维护者之一?大力推荐啊!
然后这是我这次用到的一些命令,在这里存个档:
1. insert a picture
\usepackage{graphicx}
\graphicspath{{./figs/}}
\includegraphics[width=100pt]{vfk}
2. 居中
\begin{center}
\end{center}
3. 字号
\tiny
\scriptsize
\footnotesize
\small
\normalsize
\large
\Large
\LARGE
\huge
\Huge
4. buff
\textbf{文字}
\emph{文字}
5. 换页
\clearpage
\newpage
6. 原样输出
\begin{verbatim}
\end{verbatim}
7. gif
\usepackage{animate}
\animategraphics[loop,autoplay,width=200pt]{12}{blo-}{0}{119}
8. 段落缩进
\usepackage{indentfirst}
\setlength{\parindent}{\ccwd}
9. beamer暂停
\pause
10. 行间距调整
\vspace{10pt}
11. 多行公式
$\begin{aligned}
\sum\limits_{i = 1}^{n}{k \mod i} & = \sum\limits_{i = 1}^{n}{(k - \lfloor \frac{k}{i} \rfloor \cdot i)} \\
& = n \cdot k - \sum\limits_{i = 1}^{n}{\lfloor \frac{k}{i} \rfloor \cdot i}
\end{aligned}$
带编号的话就去掉"ed"
单行不带编号:\notag
12. 列表
\usepackage{enumerate}
\begin{enumerate}[1.]
\item
\end{enumerate}
13. 插入链接
\href{https://233.com}{233}
14. 分栏
\usepackage{multicol}
\begin{multicols}{3}
\tableofcontents
\end{multicols}
15. 公式编号
\begin{equation}
233 = 233
\end{equation}
16. 文章内引用
\begin{equation}
233
\label{convolution}
\end{equation}
\eqref{convolution}
17. 空格
\qquad
\quad
18. 取模
$a^{n!} \pmod{p}$
19. 证毕
\qed
20. 整段缩进
\begin{enumerate}[\hspace{15mm}]
\item 666
\item 233
\end{enumerate}
21. 反斜杠
\usepackage{slashed}
$\slashed{\le}$
22. 数学公式字体大小
\textstyle{233}
\displaystyle
\scriptstyle
\scriptscriptstyle
【算法笔记】Kosaraju算法
前言
今天考了一套$Claris$的题
$T1$就是$Claris$用$bitset$配合这个算法把求$SCC$优化到了$\frac{n^2}{32}$
吓得我赶紧来学了学
算法概述
$step \ 1.$ DFS一遍,记录下后序遍历的顺序
$step \ 2.$ 沿后续遍历的逆序、沿反向边再DFS一遍,每一个连通块即为一个SCC
算法解释
设原图为图$G$,将$SCC$缩点后的新图为$G’$
第一遍$DFS$保证了在若某个强连通分量$A$在$G’$中是另一个强连通分量$B$的祖先
那么在后续遍历的逆序中至少存在一个点$A$中的点在$B$中所有点的前面
这样在第二次$DFS$的时候,因为是逆序,所以只能往$G’$中的祖先走
又因为祖先的$SCC$已经标记过了,所以刚好把当前$SCC$搞完,不会有多
代码实现
int scc_cnt, vis[N];
vector<int> scc_cnt[N], que;
void DFS0(int w) {
vis[w] = 0;
for (int i = head[w]; i; i = nxt[i]) {
if (!vis[to[i]]) {
DFS0(to[i]);
}
}
que[++tot] = w;
}
void DFS1(int w) {
scc[scc_cnt].push_back(w);
vis[w] = 1;
for (int i = rev_head[w]; i; i = nxt[i]) {
if (!vis[to[i]]) {
DFS1(to[i]);
}
}
}
void solve() {
que.clear();
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
DFS0(i);
}
}
scc_cnt = 0;
memset(vis, 0, sizeof(vis));
for (int i = (int)que.size() - 1; ~i; i--) {
if (!vis[que[i]]) {
scc_cnt++;
DFS1(que[i]);
}
}
}
使用$bitset$优化
这货复杂度是$O(m)$的
不难发现算法瓶颈在查找与某个点相邻的所有点中还没有被访问过的点
这个可以用$bitset$压位并配合__builtin开头的系列函数优化到$O(\frac{n^2}{32})$
例题的话,可以参考:友好城市
【算法笔记】Burnside引理与Pólya定理
前言
昨天hht来给窝萌增长了姿势水平
hht真的好神啊!伏地膜!
问:“你搞OI时如何平衡高考与竞赛”
hht:“我不用学习也能考很好,我在高一的时候已经把高中内容看完了”
正文
hht主要讲了Burnside引理的不完全证明和用Burnside引理推出Pólya定理
下面主要围绕这两方面来讨论
Burnside引理的不完全证明
有一个前置结论hht没有证明,说是需要引入很多无关的概念:
$|Z_k| \cdot |E_k| = |G|$
其中$|E_k|$表示一个等价类的大小,$|Z_k|$表示作用在这个等价类上使等价类不变的置换的数量
这个引理的证明似乎要用到群里边的轨道?我们可以参见这里:https://en.wikipedia.org/wiki/Group_action#Orbits_and_stabilizers
以下的内容建立在我们认为这个引理是正确的基础上
我们先来看一看Burnside引理的形式:$N = \frac{1}{|G|} \sum\limits_{g \in G}{\chi (g)}$
那么我们只需要证明:$N \cdot |G| = \sum\limits_{g \in G}{\chi (g)}$
对于$\sum\limits_{g \in G}{\chi (g)}$,我们实际上是先枚举置换,再枚举染色情况,再看是不是一个不动点
我们考虑换一个枚举顺序,我们枚举所有的染色情况,然后看有多少置换可以使这个染色情况成为不动点
那么这不就是$|Z_k| \cdot |E_k|$吗?于是$N \cdot |G| = \sum{|Z_k| \cdot |E_k|} = N \cdot G$,得证
使用Burnside引理推导Pólya定理
我们还是考虑枚举置换
如果一个置换可以使一种染色情况成为不动点
那么这个置换的每一个循环节只能被染成同一种颜色
所以每一种置换$g$我们有$k^{m(g)}$种染色方案($k$为可用的颜色数,$m(g)$为置换$g$的循环节)
于是我们就不用枚举所有的染色情况了,可以直接用$k^{m(g)}$计算
于是Pólya定理的公式就变成了$N = \frac{1}{|G|} \sum\limits_{g \in G}{k^{m(f)}}$
这个证明过程也非常直观地给出了Pólya定理不能解决带有颜色限制的染色问题的原因
【算法笔记】后缀自动机的基础应用
今天给我校高一神犇讲SAM _(:з」∠)_
做了个课件,顺便扔上来
suffix_automaton_practice
—————————— UPD 2017.3.21 ————————————
Menci最近写了一篇非常妙妙的Tutorial:https://oi.men.ci/suffix-automaton-notes/
以后终于不用看陈老师的PPT了!
【算法笔记】上下界网络流问题
无源汇可行流
-
问题分析:
因为只比传统网络流多了下界,所以考虑单独考虑下界的流量 -
解决方案:
于是原来的边拆为上界为min的边并强行满流,和上界为max - min的边。
但这样可能会出现流量不平衡的状况,及一个点流入的流量不等于流出量。
于是单独增加源汇点,构造一个完全等价的网络流问题
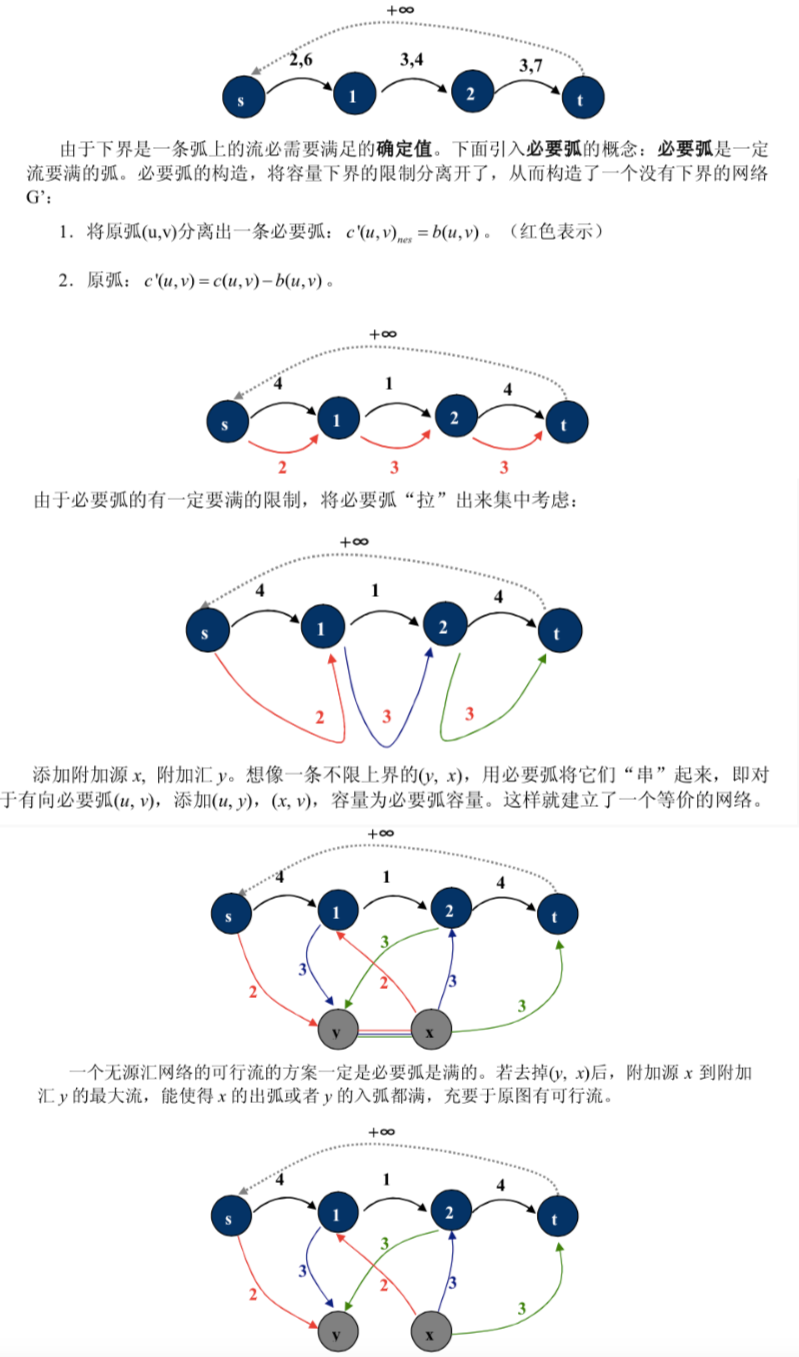
至此我们已经将问题转化为传统网络流问题,直接求解即可。
如何判断是否有可行流的根据也显而易见了:\( Max\_Flow = = \sum {Min\_Flo{w_i}}\)
有源汇可行流
-
问题分析:
有源汇意味着有一对点的流量不守恒,就是这一对点使其于无源汇可行流问题有了差别
于是我们考虑去掉这个不同点,将其转化为无源汇可行流 -
解决方案
我们注意到,将源汇点连上一条容量INF的边之后,所有的点流量都守恒了
换一句话来说我们将其转化为了无源汇可行流问题,使用上文所述方法求解即可
有源汇最大流/最小流
-
通解通法:
观察可行流的解决方案,不难发现我们控制我们人为增加的那条边的容量即可控制最大流的容量
所以我们可以二分最大流/最小流,之后进行可行流判断,再之后根据结果进行调整即可 -
最小流的高效算法:
先不连t-s的那条容量为INF的边,先跑一次附加源汇的最大流
连t-s的那条边,在残量网络上继续跑附加源汇最大流
此时t-s那条边的流量是最小的,使用上文所述方法判断其是否为可行流即可 -
最大流的高效算法
连t-s的那条容量为INF的边,跑一次附加源汇最大流
连t-s的那条边,在残量网络上继续跑s-t的最大流
此时t-s那条边的流量是最小的,使用上文所述方法判断其是否为可行流即可
【算法笔记】圆的反演
先来挖坑:
例题一:http://acm.hdu.edu.cn/showproblem.php?pid=4773
题解一:http://wangzhpp.org/?p=106
例题二:https://www.codechef.com/problems/NTHCIR
题解二:http://pppfish.com/archives/1609
例题二的中文题面:http://oi.cyo.ng/wp-content/uploads/2016/10/NTHCIR.pdf
—– UPD 2016.10.17 —–
例题一的题解:http://oi.cyo.ng/?p=1738
例题二的题解:http://oi.cyo.ng/?p=1740
ps:感觉最近这么颓废,吃枣药丸
【算法笔记】数位DP
昨天以专题的形式再一次加强了数位DP
主要是以zky神犇的这一篇讲稿作为主线:
http://oi.cyo.ng/wp-content/uploads/2016/10/number_dp_by_zky.ppt
这一次最主要的收获就是学到了新的代码实现方式
之前一直是以预处理+询问的方式来写代码
这样的话,对于多组询问来讲,时间复杂度还不错
但代码实现复杂度简直没法接受
且对于部分题目,这样写起来会超级麻烦
新的写法无论实在时间复杂度还是编程复杂度上都很优越
以后应该会以这种代码作为主力辣!
给个参考:http://oi.cyo.ng/?p=1519
至于解题能力的话,似乎数位DP的要求不高?
不过能和AC自动机搞一起还是挺好玩哒:http://oi.cyo.ng/?p=1534
【算法笔记】再再看线性基
这一次是以专题的形式
主要以这份题单作为主线:http://www.cnblogs.com/joyouth/p/5645682.html
感觉对于线性基已经理解透了?(大雾)
不过还是不会拟阵…
![]()


