相关链接
题目传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=3577
神犇题解:http://www.cnblogs.com/clrs97/p/4403242.html
解题报告
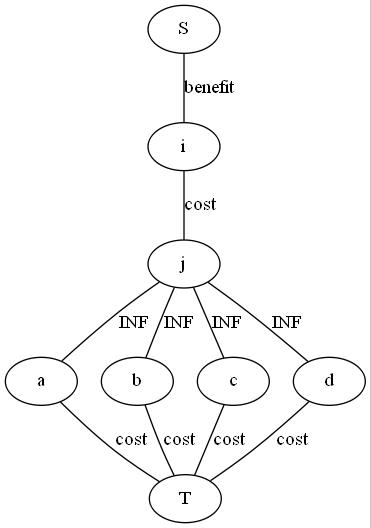
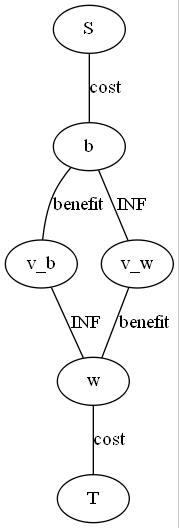
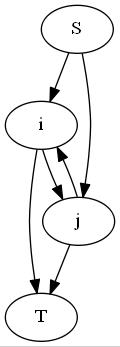
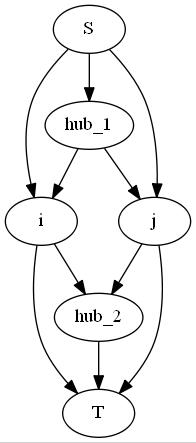
之前一直都是线段树优化建图
这题需要用$ST$表来优化建图
Code
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int INF = 1e9;
const int N = 500000;
const int M = 2000000;
int S,T,E,tot,A,B,Y,X,n2[2][70][70][8];
int head[N],nxt[M],to[M],flow[M],n1[2][70][70];
inline int read() {
char c=getchar(); int f=1,ret=0;
while (c<'0'||c>'9') {if(c=='-')f=-1;c=getchar();}
while (c<='9'&&c>='0') {ret=ret*10+c-'0';c=getchar();}
return ret * f;
}
inline void AddEdge(int u, int v, int f) {
assert(u); assert(v);
to[++E] = v; nxt[E] = head[u]; head[u] = E; flow[E] = f;
to[++E] = u; nxt[E] = head[v]; head[v] = E; flow[E] = 0;
}
class NetworkFlow{
int dis[N],cur[N];
queue<int> que;
public:
inline int MaxFlow() {
int ret = 0;
while (BFS()) {
memcpy(cur, head, sizeof(cur));
ret += DFS(S, INF);
}
return ret;
}
private:
inline bool BFS() {
memset(dis, 60, sizeof(dis));
dis[S] = 0;
for (que.push(S); !que.empty(); que.pop()) {
int w = que.front();
for (int i = head[w]; i; i = nxt[i]) {
if (flow[i] && dis[to[i]] > INF) {
dis[to[i]] = dis[w] + 1;
que.push(to[i]);
}
}
}
return dis[T] <= INF;
}
inline int DFS(int w, int f) {
if (w == T) {
return f;
} else {
int ret = 0;
for (int &i = cur[w]; i; i = nxt[i]) {
if (flow[i] && dis[to[i]] == dis[w] + 1) {
int tmp = DFS(to[i], min(f, flow[i]));
ret += tmp; f -= tmp;
flow[i] -= tmp; flow[i ^ 1] += tmp;
if (!f) {
break;
}
}
}
return ret;
}
}
}Dinic;
int main() {
#ifdef DBG
freopen("11input.in", "r", stdin);
#endif
X = read(); Y = read();
A = read(); B = read();
S = ++tot; T = ++tot;
E = 1;
for (int i = 1; i <= X; ++i) {
for (int j = 1; j <= Y; ++j) {
n1[0][i][j] = ++tot;
n1[1][i][j] = ++tot;
AddEdge(n1[0][i][j], n1[1][i][j], read());
}
}
for (int i = X; i; --i) {
for (int j = Y; j; --j) {
for (int a = 0, len = 1; i + len - 1 <= X && j + len - 1 <= Y; ++a, len <<= 1) {
n2[0][i][j][a] = ++tot;
n2[1][i][j][a] = ++tot;
if (!a) {
AddEdge(n2[0][i][j][a], n1[0][i][j], INF);
AddEdge(n1[1][i][j], n2[1][i][j][a], INF);
} else {
int llen = len >> 1;
AddEdge(n2[0][i][j][a], n2[0][i][j][a - 1], INF);
AddEdge(n2[0][i][j][a], n2[0][i + llen][j][a - 1], INF);
AddEdge(n2[0][i][j][a], n2[0][i][j + llen][a - 1], INF);
AddEdge(n2[0][i][j][a], n2[0][i + llen][j + llen][a - 1], INF);
AddEdge(n2[1][i][j][a - 1], n2[1][i][j][a], INF);
AddEdge(n2[1][i][j + llen][a - 1], n2[1][i][j][a], INF);
AddEdge(n2[1][i + llen][j][a - 1], n2[1][i][j][a], INF);
AddEdge(n2[1][i + llen][j + llen][a - 1], n2[1][i][j][a], INF);
}
}
}
}
for (int i = 1, w, x1, x2, y1, y2, p0, p1; i <= A; ++i) {
p0 = ++tot; p1 = ++tot;
w = read();
x1 = read(); y1 = read();
x2 = read(); y2 = read();
AddEdge(S, p0, INF);
AddEdge(p0, p1, w);
int len = x2 - x1 + 1, lg = 0, d = 1;
for (; (d << 1) <= len; lg++, d <<= 1);
AddEdge(p1, n2[0][x1][y1][lg], INF);
AddEdge(p1, n2[0][x1][y2 - d + 1][lg], INF);
AddEdge(p1, n2[0][x2 - d + 1][y1][lg], INF);
AddEdge(p1, n2[0][x2 - d + 1][y2 - d + 1][lg], INF);
}
for (int i = 1, w, x1, x2, y1, y2, p0, p1; i <= B; ++i) {
p0 = ++tot; p1 = ++tot;
w = read();
x1 = read(); y1 = read();
x2 = read(); y2 = read();
AddEdge(p0, p1, w);
AddEdge(p1, T, INF);
int len = x2 - x1 + 1, lg = 0, d = 1;
for (; (d << 1) <= len; lg++, d <<= 1);
AddEdge(n2[1][x1][y1][lg], p0, INF);
AddEdge(n2[1][x1][y2 - d + 1][lg], p0, INF);
AddEdge(n2[1][x2 - d + 1][y1][lg], p0, INF);
AddEdge(n2[1][x2 - d + 1][y2 - d + 1][lg], p0, INF);
}
assert(tot < N);
assert(E < M);
printf("%d\n", Dinic.MaxFlow());
return 0;
}