相关链接
题目传送门:https://www.codechef.com/NOV15/problems/TREEP
中文题面:http://www.codechef.com/download/translated/NOV15/mandarin/TREEP.pdf
官方题解:https://discuss.codechef.com/questions/76897/treep-editorial
题目大意
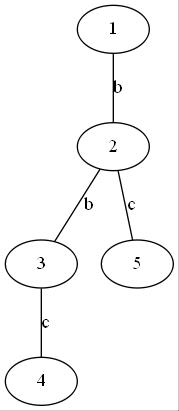
给定一个$n(n \le 200000)$个结点的树,每条边上有一个小写字母
定义$Str_{u,v}$为从$u$走到$v$将路径上的小写字母按顺序拼起来组成的字符串
给定$m(m \le 200000)$个操作,操作分两类:
- 输入$u,v$,询问$Str_{u,v}$的循环节最短为多长
- 输入$u,v,c$,表示将$u \to v$这条边上的字符改成$c$
解题报告
这么奇怪的题目,一看就只能是$Hash$来做
我们不难发现,若循环节为$l$,串长$len$,那么$\forall x \in (l,len]$若$x \equiv 0(\bmod l)$则$x$也是循环节
于是如果我们可以$O(\log n)$判定$l$是不是原串的循环节,我们就可以在$O(n \log^2 n)$的时间复杂度内解决这个问题了
我们发现,若是循环节,那么开头那一段的$Hash$值不仅可以整除整个串的$Hash$值,而且等于一个等比数列
于是我们就可以用BIT维护一个到根的前缀和,然后将判定优化到$O(\log n)$
Code
这是考试的代码,似乎没写多组数据,CC上交不了QwQ
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 200009;
const int M = N << 1;
const int SED = 37;
const int MOD = 1000000009;
int n,m,head[N],to[M],nxt[M],cost[M],dep[N],beg[N],END[N];
int POW[M],tot,pri[N],vis[N],sur[N],fa[N][20],val[N];
char pat[5];
inline int read() {
char c=getchar(); int ret=0,f=1;
while (c<'0'||c>'9') {if(c=='-')f=-1;c=getchar();}
while (c<='9'&&c>='0') {ret=ret*10+c-'0';c=getchar();}
return ret*f;
}
inline void AddEdge(int u, int v, int c) {
static int E = 1; cost[E+1] = cost[E+2] = c;
to[++E] = v; nxt[E] = head[u]; head[u] = E;
to[++E] = u; nxt[E] = head[v]; head[v] = E;
}
class FenwickTree{
#define lowbit(x) ((x)&(-(x)))
int sum[N];
public:
inline void modify(int l, int r, int v) {
for (int i=l-1;i;i-=lowbit(i)) sum[i] = (sum[i] - v) % MOD;
for (int i=r;i;i-=lowbit(i)) sum[i] = (sum[i] + v) % MOD;
}
inline int query(int p) {
int ret = 0; p = beg[p];
for (int i=p;i<=n;i+=lowbit(i))
ret = (ret + sum[i]) % MOD;
return (ret + MOD) % MOD;
}
}up,dw;
inline void prework() {
POW[0] = sur[1] = 1;
for (int i=1;i<M;i++) POW[i] = (LL)POW[i-1] * SED % MOD;
for (int i=2;i<N;i++) {
if (!vis[i]) pri[++tot] = i, sur[i] = i;
for (int j=1;j<=tot&&i*pri[j]<N;j++) {
vis[i*pri[j]] = 1; sur[i*pri[j]] = pri[j];
if (i % pri[j] == 0) break;
}
}
}
inline int LCA(int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
for (int j=19;~j;j--) if (dep[fa[u][j]]>=dep[v]) u=fa[u][j];
if (u == v) return u;
for (int j=19;~j;j--) if (fa[u][j]!=fa[v][j]) u=fa[u][j],v=fa[v][j];
return fa[u][0];
}
void DFS(int w, int f) {
static int dfs_cnt = 0;
beg[w] = ++dfs_cnt;
fa[w][0] = f; dep[w] = dep[f] + 1;
for (int i=head[w];i;i=nxt[i]) {
if (to[i] != f) {
val[to[i]] = cost[i];
DFS(to[i], w);
}
}
END[w] = dfs_cnt;
up.modify(beg[w], END[w], (LL)val[w] * POW[n-dep[w]+1] % MOD);
dw.modify(beg[w], END[w], (LL)val[w] * POW[dep[w]] % MOD);
}
inline int FA(int u, int k) {
for (int t=0;k;k>>=1,t++)
if (k&1) u = fa[u][t];
return u;
}
inline int query(int u, int v, int lca, int k) {
if (dep[u] - dep[lca] >= k) {
int ret = (up.query(u) - up.query(FA(u, k))) % MOD;
return (((LL)ret * POW[dep[u]-1] % MOD) + MOD) % MOD;
} else {
int ret = (up.query(u) - up.query(lca)) % MOD;
ret = (LL)ret * POW[dep[u] - 1] % MOD;
int res = dep[u] + dep[v] - (dep[lca] << 1) - k;
res = (dw.query(FA(v, res)) - dw.query(lca)) % MOD;
res = (LL)res * POW[n + dep[u] - (dep[lca] << 1) - 1] % MOD;
return ((res + ret) % MOD + MOD) % MOD;
}
}
inline int Pow(int w, int t) {
int ret = 1;
for (;t;t>>=1,w=(LL)w*w%MOD)
if (t&1) ret=(LL)ret*w%MOD;
return ret;
}
inline int query(int u, int v) {
int lca = LCA(u, v); tot = 0;
int len = dep[u] + dep[v] - (dep[lca] << 1);
int STA = query(u, v, lca, len), ori = len;
for (int c,w=len;c=sur[w],w>1;) {
pri[++tot] = c; vis[tot] = 0;
for (;w%c==0;w/=c) vis[tot]++;
}
for (int i=1,sta,cur,PRI;i<=tot;i++) {
PRI = pri[i];
for (int j=1;j<=vis[i];j++) {
sta = (LL)(Pow(POW[len/PRI], ori/len*PRI) - 1) * Pow(POW[len/PRI]-1, MOD-2) % MOD;
cur = (LL)STA * Pow(query(u, v, lca, len / PRI), MOD-2) % MOD;
if (sta==cur) len /= PRI;
else break;
}
}
return len;
}
int main() {
prework();
n = read();
for (int i=1,u,v;i<n;i++) {
u = read(); v = read();
scanf("%s",pat+1);
AddEdge(u, v, pat[1]-'a'+1);
}
DFS(1, 1);
for (int j=1;j<20;j++) {
for (int i=1;i<=n;i++) {
fa[i][j] = fa[fa[i][j-1]][j-1];
}
}
m = read();
for (int i=1,u,v,c;i<=m;i++) {
if (read() == 1) {
u = read(); v = read();
printf("%d\n",query(u, v));
} else {
u = read(); v = read();
if (dep[u] > dep[v]) swap(u, v);
scanf("%s",pat+1); c = pat[1]-'a'+1;
if (c == val[v]) continue;
up.modify(beg[v], END[v], (LL)(c - val[v]) * POW[n-dep[v]+1] % MOD);
dw.modify(beg[v], END[v], (LL)(c - val[v]) * POW[dep[v]] % MOD);
val[v] = c;
}
}
return 0;
}