相关链接
题目传送门:https://www.hackerrank.com/challenges/unique-colors
题目大意:http://paste.ubuntu.com/23686184/
官方题解:https://www.hackerrank.com/challenges/unique-colors/editorial
解题报告
Ⅰ.点分治的做法 \(O(n\log (n))\)
先考虑一种较为简单的情况:只有一种颜色
询问有多少对节点间至少存在一个点被染色直接考虑点分治的做法的话
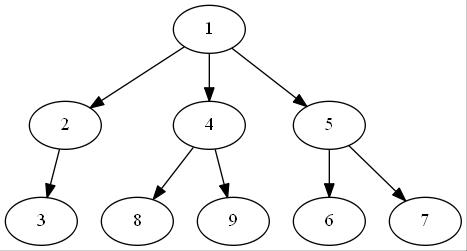
设当前的分治点为1
定义\({T_i}\)为点i的子树中到1号点的路径上有点被染色的点的数量
定义\({S_i}\)为点i的子树中点的个数
考虑此时对 点3 的贡献:
- 点3 到 点1 的简单路径上没有染色点
那么贡献为\({T_1} – {T_3}\)- 点3 到点1 的简单路径上有染色点
那么贡献为\({S_1} – {S_2}\)这样的话,只有一种颜色的情况就解决了
现在考虑有多种颜色:不难发现对于一个固定点i,颜色只需要分两类:
1. 到分支点的路径上出现过该颜色
2. 到分治点的路径上没有出现过该颜色这样的话,我们发现只需要一次DFS就可以解决这个问题
于是就可以使用点分治解决这个问题啦!
Ⅱ. DFS序的做法 \(O(n)\)
先来考虑一个简单一点的版本:假如这货是在序列上
考虑每一种颜色单独处理的话,就是将序列分成几块,每一块的贡献不同
现在重新考虑树上的版本,其实也是把整个树分成好几块
酱紫的话,我们唯一需要解决的就是如何给树上一个连通块统一加上一个数
我们发现我们可以先搞出一个最小的包含“需要更改的连通块”的子树
然后去掉一些子树来删掉多余的部分
子树操作的话,在DFS序上是连续的,于是打差分就好
因为题目的特殊性,不难发现需要删掉的子树总共只会有\(O(n)\)个
于是此题就 \(O(n)\) 辣!

88029 833313This article is dedicated to all those who know what is billiard table; to all those that do not know what is pool table; to all people who want to know what is billiards; 592857
761683 228747IE still is the market chief and a big element of other folks will omit your great writing because of this problem. 756825
560116 129518Um, consider adding pictures or much more spacing to your weblog entries to break up their chunky look. 176055
418539 166239Today, while I was at work, my sister stole my iPad and tested to see if it can survive a thirty foot drop, just so she can be a youtube sensation. My iPad is now destroyed and she has 83 views. I know this is entirely off topic but I had to share it with someone! 611355
479682 857795Spot ill carry on with this write-up, I truly feel this internet site requirements an excellent deal a lot more consideration. Ill oftimes be once far more to see far a lot more, numerous thanks that info. 541190
135502 672230my grandmother is always into herbal stuffs and she always say that ayurvedic medicines are the top stuff 590139
82604 12729Outstanding read, I just passed this onto a colleague who was performing a bit research on that. And he in fact bought me lunch as I found it for him smile So let me rephrase that: Thank you for lunch! 922739
562374 532194Hello! I would wish to supply a large thumbs up for your outstanding info you could have here about this post. Ill be coming back to your blog site for further soon. 277559
Write more, thats all I have to say. Literally, it seems as though you relied on the video to make your point. You definitely know what youre talking about, why waste your intelligence on just posting videos to your blog when you could be giving us something informative to read?
501926 923610An intriguing discussion will probably be worth comment. I believe which you can write read a lot more about this topic, could properly undoubtedly be a taboo topic but usually folks are inadequate to chat on such topics. To a higher. Cheers 65812
238277 702992Thanks for this wonderful post! It has long been quite beneficial. I wish that you will carry on posting your wisdom with us. 223999
582929 654004 I discovered your blog internet site on google and check several of your early posts. Continue to keep up the very very good operate. I just additional up your RSS feed to my MSN News Reader. Seeking forward to reading far more from you later on! 457468
Thanks a ton for sharing your well put together web site.|
Excellent post. I was checking constantly this blog and I’m impressed! Extremely useful info specially the last part 🙂 I care for such info much. I was looking for this certain info for a long time. Thank you and good luck.